1、常见的进制

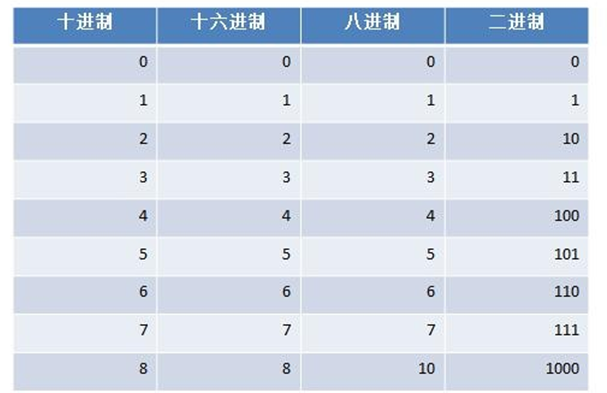
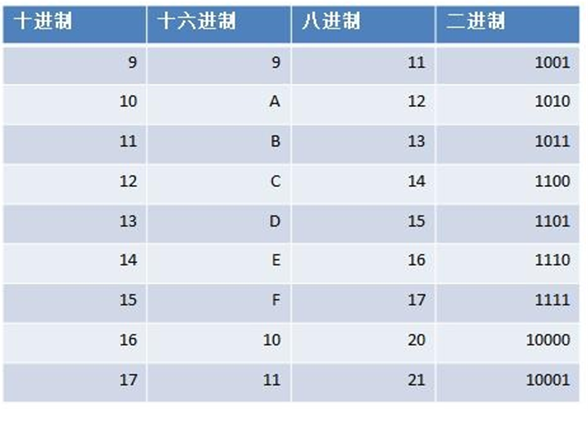
2、其它进制转十进制

2.1 二进制转十进制

二进制转十进制的转换原理：从二进制的右边第一个数开始，每一个乘以2的n次方，n从0开始，每次递增1。然后得出来的每个数相加即是十进制数。

1110=1*2*2*2+1*2*2+1*2+0*1=14

2.2 八进制转十进制

八进制转十进制的转换原理：从八进制的右边第一个数开始，每一个乘以8的n次方，n从0开始，每次递增1。然后得出来的每个数相加即是十进制数。

0156 = 1×8^2 + 5×8^1 + 6×8^0=110

2.3 十六进制转十进制

16进制就是逢16进1，但我们只有0~9这十个数字，所以我们用A，B，C，D，E，F这六个字母来分别表示10，11，12，13，14，15。字母不区分大小写。

十六进制转十进制的转换原理：从十六进制的右边第一个数开始，每一个乘以16的n次方，n从0开始，每次递增1。然后得出来的每个数相加即是十进制数。

0x2AF5换算成10进制:
2AF5=2*16*16*16+10*16*16+15*16+5=10,997

3、十进制转其他进制

3.1 十进制转二进制

173转二进制

3.2 十进制转八进制

136转成八进制0210

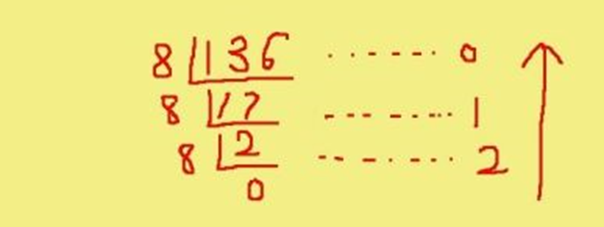
3.3 十进制转十六进制

136转成十六进制是0x88

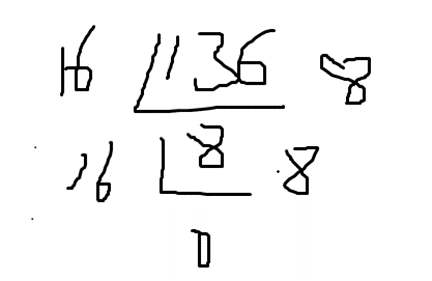
4、 二进制转其它进制

4.1 二进制转八进制

方法为：将二进制数每三位一组（从低位开始组合），转成对应的八进制数即可。

11011110=0336

011=3

011=3

110=6

4.2 二进制转十六进制

方法：将二进制数每四位一组（从低位到高位组合），转成对应的十六进制数即可。

11011110=DE

5、其他进制转二进制

5.1 八进制转二进制

方法：将八进制数每1位，转成对应的一个3位的二进制数即可

0567=101110111

5.2 十六进制转二进制

方法：将16进制数每1位，转成对应的一个四位的二进制数即可。

0x567=010101100111

6、位运算符和位算符

6.1 二进制在运算中的说明

二进制是逢2进位的进位制，0、1 是基本算符。

现代的电子计算机技术全部采用的是二进制，因为它只使用 0、1 两个数字符号，非常简单方便，易于用电子方式实现。计算机内部处理的信息，都是采用二进制数来表示的。二进制（Binary）数用0和 1 两个数字及其组合来表示任何数。进位规则是“逢 2 进 1”，数字 1 在不同的位上代表不同的值， 按从右至左的次序，这个值以二倍递增。

在计算机的内部，运行各种运算时，都是以二进制的方式来运行。

6.2 源码、补码、反码

6.3 位运算符介绍

位运算符对整数在内存中的二进制位进行操作。

分别是”按位与&、按位或|、按位异或^,它们的运算规则是：

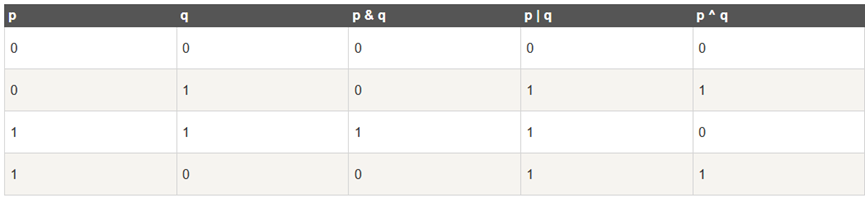
按位与& ： 两位全为１，结果为 1，否则为 0

按位或| : 两位有一个为 1，结果为 1，否则为 0

按位异或 ^: 两位一个为 0,一个为 1，结果为 1，否则为 0

6.4 位移运算符

>>、<< 右移和左移,运算规则:
右移运算符>>：低位溢出,符号位不变,并用符号位补溢出的高位
左移运算符<<: 符号位不变,低位补 0
a := 1 >> 2	// 0000 0001 =>0000 0000 = 0
c := 1 << 2	// 0000 0001 ==> 0000 0100 => 4